Olá amigos!

Nesta semana tiraremos a dúvida de um de nossos leitores, que quer saber um pouco mais sobre o nosso sistema de numeração! Para nos ajudar a responder, eu convidei o professor de Matemática Marcos Alves do nosso querido IFMG-Bambuí.

Por que quase todos os países usam uma mesma simbologia para os números? Quem e quando se inventou essa simbologia?

Por Marcos Alves de Farias (marcos.farias@ifmg.edu.br)

Num período em que antecedeu a invenção dos números, houve um tempo em que o ser humano não sabia contar. A lógica que utilizava para descrever e relacionar quantidades era a da correspondência um a um, fazendo para isso associar, por exemplo, os dedos das mãos, pedras, ossos, paus, ou quaisquer outros objetos, aos elementos que se desejasse contar.

A invenção dos números não se deu da noite para o dia, esse foi um processo que durou milênios e se deveu a necessidade de registro de quantidades excessivamente grandes para que fossem memorizadas.

Num período em que antecedeu a escrita numérica, por volta de 3.500 a.C., na região da Mesopotâmia, movidos pela necessidade de se registrar valores de transações comerciais, os Sumérios construíram um sofisticado sistema numérico sexagesimal, por meio de peças moldadas em argila, de maneira que, um cone pequeno valeria por 1 unidade; uma bola pequena, 10 unidades; um cone grande, 60 unidades; um cone grande perfurado, 600 (60x10) unidades; uma esfera, 3600 (60x60) unidades; e uma esfera perfurada, 36000 (60x60x10) unidades. Este sistema numérico também chegou a ser utilizado pelos Babilônios, sendo empregado em medidas de tempo e ângulo.

Um sistema numérico muito conhecido é o dos números romanos, que predominou na Roma antiga, mas suas origens são muito anteriores a sua própria civilização. A numeração romana é constituída pelos algarismos I=1; V=5; X=10; L=50; C=100; D=500; M=1000, que são independentes uns dos outros e sua justaposição implica, quase sempre, na soma dos valores correspondentes. A exceção da soma é quando o número anterior é menor que o posterior, situação essa que pode resultar numa subtração de valores.

Pelas suas particularidades, os números romanos são inapropriados para a realização de operações aritméticas. Contudo, com o uso cada vez menos significativo, ainda são utilizados nos dias de hoje na indicação de séculos, em nomes de papas e de reis, na numeração de capítulos de uma obra, em mostradores de relógios analógicos, na designação de congressos, feiras, olimpíadas, etc.

O sistema mais utilizado atualmente é o de numeração indo-arábico, que teve sua origem na Índia por volta de 250 a.C. e possui esse nome devido os árabes o terem trazido para a Europa Ocidental durante a Idade Média, provavelmente por meio de viajantes e comerciantes. A principal razão de boa parte do globo ter aderido a este sistema de numeração se deve a sua capacidade de representação numérica e a facilidade na realização de operações aritméticas.

Inicialmente, no sistema numérico indiano haviam apenas 9 algarismos diferentes, não havia um princípio de posição e o zero era apenas falado, mas não escrito. Contudo, quando os hindus criaram o princípio de posição e uma representação para o número zero, ao final do século VI, um salto de desenvolvimento ocorreu nos campos que envolvem a Matemática, possibilitando com isso a representação de qualquer quantidade e a criação de um sistema de numeração decimal com as operações aritméticas muito bem definidas.

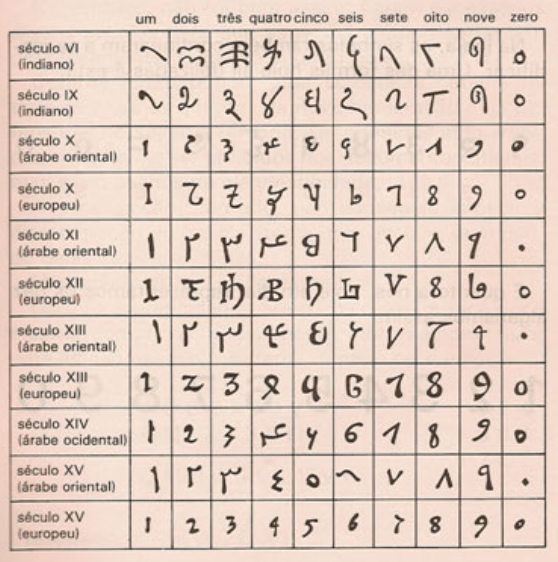
Evolução dos símbolos do sistema de numeração indo-arábico
Fonte: https://www.iejusa.com.br/cienciaetecnologia/matematica.php