Por Fernando Augusto Naves (fernando.naves@ifmg.edu.br) e

Geraldo Henrique Alves Pereira (geraldo.pereira@ifmg.edu.br).

Os mais jovens que nos perdoem, mas crescemos vendo a cena do seriado Chaves em que o personagem Quico fica feliz quando lhe é prometida uma “bola quadrada”. Afinal, seria possível existir uma bola quadrada? Matematicamente, a resposta é sim!

Antes de tudo, é preciso notar que o termo “bola” é naturalmente empregado em seu sentido geométrico intuitivo, ou seja, quando pensamos em uma bola, automaticamente vislumbramos aquele objeto de formas arredondadas que estamos acostumados a ver. Nossa noção de bola é, portanto, essencialmente concreta; e aqui, neste texto, o aproximaremos do conceito de “esfera”.

Acontece que na Matemática as coisas podem ser mais gerais, não tão intuitivas e concretas assim, vejamos!

Dois elementos são fundamentais para se definir uma esfera:

1. um ponto $C$, que será o seu centro;
2. um número $r$ positivo, que será o seu raio.

Assim, uma esfera de centro $C$ e raio $r$ é o conjunto de todos os pontos do espaço com exata distância $r$ do ponto $C$.

Então, observemos que por trás da definição de esfera está o conceito de distância. Mas como medimos a distância entre dois pontos?

Na escola aprendemos a medir/calcular "concretamente" a distância entre dois pontos quaisquer do espaço $P=(x_1,y_1,z_1)$ e $Q=(x_2,y_2,z_2)$ pela formula:

$$d(P,Q)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}.$$

Essa forma de medir a que nos acostumamos é chamada de distância euclidiana e, assim, a chamaremos de $d_{euc}$.

Usando esta maneira de calcular distâncias, o formato da esfera coincide com a que já estamos “acostumados” (geometricamente falando).

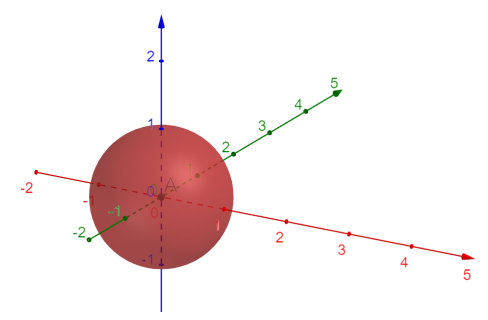
A fórmula da distância acima mede essencialmente o comprimento do segmento de reta que liga os dois pontos em questão ($P$ e $Q$). Entretanto, será essa a melhor forma de calcularmos distâncias? Na maior parte das vezes no nosso cotidiano, sim! Quando estamos interessados em medir as dimensões de um terreno ou o tamanho de uma casa, a distância euclidiana, pura e simples, se mostra a opção mais efetiva.

Mas pensemos agora em escala global. Imagine uma pessoa no Polo Norte e outra no Polo Sul. Para fins práticos, a pura e simples distância euclidiana entre elas não parece ser a melhor medida. Ou talvez quando pensamos no trajeto feito por um carro dentro da cidade. Isso nos motiva a estudar outras formas de se pensar em distâncias. 

A distância é uma função que, a cada dois pontos do espaço, nos fornece um número real. Acontece que não podemos escolher de maneira completamente arbitrária qualquer função para calcularmos distâncias, pois o absurdo seria chegarmos a distâncias negativas.

Assim, para que uma função $d$, definida num conjunto $X$, possa ser considerada uma distância, ela deve cumprir os seguintes requisitos para quaisquer pontos $A$, $B$ e $C$ de $X$:

1. $d(A,B)\geq 0$;
2. $d(A,B)=0$ se, e somente se, $A=B$;
3. $d(A,B)=d(B,A)$;
4. $d(A,C)\leq d(A,B)+d(B,C)$.

Existem diversas funções que cumprem os 4 requisitos acima. Um exemplo é a chamada distância do máximo: dados dois pontos $P = (a_1,b_1,c_1)$ e $Q = (a_2,b_2,c_2)$, a distância entre $P$ e $Q$ pode ser definida por $d_{max}(P,Q)=max \left\{|a_1-a_2|,|b_1-b_2|,|c_1-c_2|\right\}$.

Tente perceber que essa função satisfaz as propriedades acima. Por exemplo, considere os pontos $P = (1,3,−7)$ e $Q = (1,−2,5)$. Teremos, portanto:

$$d_{max}(P,Q)=max \left\{|1-1|,|3-(-2)|,|-7-5|\right\}$$ $$=max \left\{|0|,|5|,|-12|\right\}$$ $$=max \left\{0,5,12\right\}$$ $$=12.$$

Logo, neste caso, a distância entre os pontos $P$ e $Q$ é $12$. Se à distância euclidiana entre $P$ e $Q$ fizéssemos uma comparação, teríamos uma leve diferença, pois esta última vale $13$.

Usando a distância do máximo, a esfera de centro na origem $C=(0,0,0)$ e raio $1$ seria o conjunto de todos os pontos $P = (a,b,c)$ do espaço tais que

$$d_{max}(P,C)=1,$$

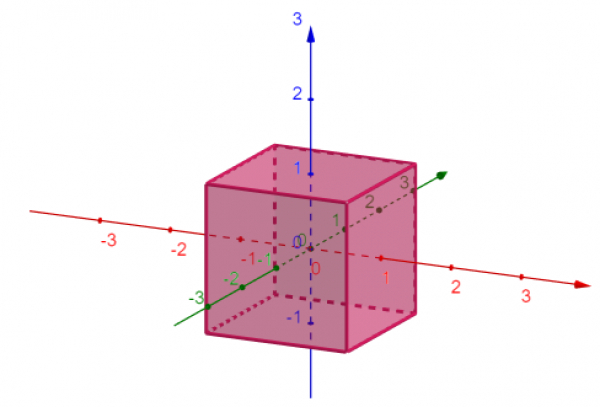
isto é, estamos procurando os pontos $P=(a,b,c)$ em que $max \left\{|a|,|b|,|c|\right\}=1$. Assim, a representação geométrica dessa esfera é:

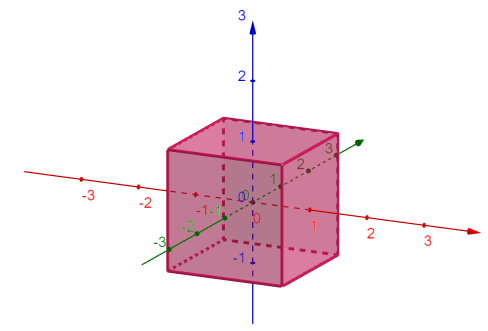
Eis a bola quadrada do Quico!