Olá caros leitores!

No texto desta semana esclareceremos uma dúvida de Matemática do nosso leitor Victor Hugo Rodrigues, que gostaria de saber quantos números primos existem! Para nos ajudar, convidamos o professor de Matemática Marcos Alves, do nosso querido IFMG - Bambuí.

Quantos números primos existem?

Por Marcos Alves de Farias (marcos.farias@ifmg.edu.br)

Para falar de números primos, primeiro, precisamos deixar claro o conceito de divisibilidade. De modo geral, para dois números inteiros $a$ e $b$, dizemos que $b$ é divisor de $a$ se existe um número inteiro $c$ tal que $a=b\times c$. Por exemplo, $2$ é divisor de $10$, uma vez que,

$$\underbrace{10}_{{\color{red}{a}}}=\underbrace{2}_{{\color{red}{b}}}\times \underbrace{5}_{{\color{red}{c}}}.$$

Assim como $3$ é divisor de $-12$, pois, pode-se escrever,

$$\underbrace{-12}_{{\color{red}{a}}}=\underbrace{3}_{{\color{red}{b}}}\times \underbrace{(-4)}_{{\color{red}{c}}}.$$

Note que, para $b\neq 0$, dizer que $b$ é divisor de $a$ significa que o resto da divisão de $a$ por $b$ é zero. Ou seja, pelo com o algoritmo da divisão, 

teríamos 

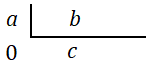o que, de acordo com os exemplos apresentados,

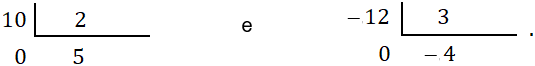
Então, de posse do conceito de divisibilidade, um número inteiro é dito primo se ele possui exatamente dois divisores positivos. Por exemplo, $2$ é um número primo, pois $1$ e $2$ são os seus únicos divisores positivos. Assim como, $-2$ também é primo, pois os seus únicos divisores positivos são também $1$ e $2$. Contudo, observe que $1$ não é primo, uma vez que, o número $1$ admite um único divisor positivo, que seria ele mesmo!

De modo geral, para qualquer número primo $p$, o seu oposto, $-p$, é primo também. Contudo, devido apenas a questão do sinal, o estudo dos números primos acaba tendo o seu foco nos primos positivos.

A seguir, encontram-se listados todos os números primos positivos até $100$:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.

Agora, respondendo à pergunta, sobre quantos números primos existem, a resposta é infinitos. Como prova desse fato, podemos citar uma demonstração dada pelo matemático grego Euclides, que viveu a cerca de 300 a. C. Nesta prova, Euclides mostra que a quantidade de números primos não pode ser finita, pois caso o fosse, todos os números primos poderiam ser apresentados, para ilustrar, digamos: 

$$p_1,\textrm{ } p_2,\textrm{ } p_3,\ldots ,\textrm{ } p_n.$$

Contudo, ao se tomar o número

$$p=p_1\times p_2\times p_3\times \ldots \times p_n+1$$

observamos que $p$ não é divisível por nenhum dos números primos $p_1$, $p_2$, $p_3$, …      e $p_n$. Pois, por exemplo, caso $p$ fosse divisível por $p_1$, teríamos, pelo fato do produto $p_1\times p_2\times p_3\times \ldots \times p_n$, obviamente, ser divisível por $p_1$, que o número $1$ seria também divisível por $p_1$, uma vez que, pela relação acima, obtemos:

$$\underbrace{p}_{{\color{red}{\textrm{é divisível por }p_1}}}-\textrm{   }\underbrace{p_1\times p_2\times p_3\times \ldots \times p_n}_{{\color{red}{\textrm{é divisível por }p_1}}}=1.$$

Mas, sendo $1$ e $-1$ os únicos divisores de $1$, tal fato nos levaria a concluir que $p_1=1$ ou $p_1=-1$, o que sabemos não serem primos. Deste modo, como tal raciocínio se aplica a todos os outros primos, $p_2$, $p_3$, … e $p_n$, somos levados a concluir que, de fato, $p$ não é divisível por nenhum dos números $p_1$, $p_2$, $p_3$, … e $p_n$. Então, sendo esses todos os primos, como $p$ não é divisível por nenhum deles, conclui-se que $p$ é um número primo também! O que não seria possível, pois ao supor que havia uma quantidade finita de primos, foi afirmado que os números

$$p_1,\textrm{ } p_2,\textrm{ } p_3,\ldots ,\textrm{ } p_n$$

eram todos os primos existentes, e dentre esses números não consta o $p$.

Portanto, a única possibilidade é a conclusão de que não podem haver finitos primos! Pois caso houvessem, sempre surgiria um novo primo que não está nesta lista! Deste modo, Euclides assegura em sua demonstração que a quantidade de números primos é infinita!