Por Letícia Alves da Silva (leticia.alves@ifmg.edu.br); Marcos Alves de Farias; Samuel Leandro Fonseca Amaral; Wesley Isidoro de Paula.

Nos últimos anos, surgiu um novo tipo de Geometria, a chamada Geometria Fractal, que consegue explicar alguns fenômenos não estudados na Geometria Euclidiana. A Geometria Fractal tem aplicações em áreas que vão além da Matemática, como na Medicina, na Arte, na Meteorologia, na Biologia, na Física, na Astronomia, etc.

A origem do termo fractal vem do adjetivo latino fractus, que significa quebrar. O termo Fractal foi criado pelo cientista Benoit Mandelbrot, que foi um matemático polonês nacionalizado francês. Segundo Mandelbrot, os Fractais são formas igualmente complexas no detalhe e na forma global.

A definição de Fractal pode ser encarada como um processo de recursão, onde cada aresta (lado) do objeto é dividida em r partes geometricamente iguais, obtendo-se o coeficiente de redução k, onde k=1/r. Nesse processo, pode-se definir como N o número de objetos iguais resultantes do processo recursivo de subdivisão. Dessa forma, o processo recursivo acontece ao pegar um objeto, dividi-lo em partes iguais e, para cada fração obtida, a divisão em partes iguais se repete sucessivamente.

Para exemplificar tal comportamento, considere como objeto de estudo o segmento de reta representado na Figura 1. O objeto, sem nenhuma iteração, compõe a Iteração Inicial ou Iteração 0 do processo recursivo. Na Iteração 1, divide-se o segmento em três partes iguais (r=3), obtendo-se 3 segmentos de reta idênticos.

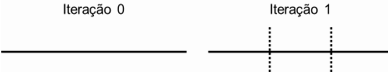
Figura 1 - Exemplo de processo recursivo: segmento de reta.
Fonte: Autores (2023)

Percebe-se que o coeficiente k de redução é ⅓ e o número N de objetos resultantes do processo recursivo é 3. Logo, existe uma relação de igualdade para o número r de divisões realizadas no objeto e o número N de objetos resultantes do processo recursivo, o que não acontece se o objeto de estudo for um quadrado, onde as iterações estão representadas na Figura 2.

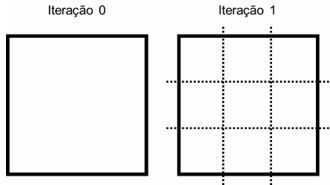
Figura 2 - Exemplo de processo recursivo: quadrado.
Fonte: Autores (2023)

Ao dividir os segmentos em três partes iguais (r=3), obtém-se 9 quadrados idênticos, representados na Iteração 1. Assim, o coeficiente k de redução é ⅓ e o número N de objetos resultantes do processo recursivo é 9.

Os exemplos apresentados são base para entendimento do comportamento fractal, onde o objeto passa por um processo de recursão. Em 1904, o matemático Helge von Koch (1870-1924) publicou o que foi chamado popularmente de Floco de Neve de Koch, representado na Figura 3, que é um fractal cujo processo recursivo foi realizado em um triângulo equilátero.

Figura 3 - Floco de Neve de Koch
Fonte: https://www.researchgate.net/figure/The-Helge-von-Koch-curve_fig1_340056482

Partindo de um triângulo equilátero, pode-se dividir cada lado em três partes iguais, excluir a parte do meio e substituí-la por um outro triângulo equilátero, sem a sua base. Repetindo a iteração, pode-se dividir novamente cada lado da nova figura em três partes iguais, excluir as partes do meio e substituí-las por triângulos equiláteros, sem a base. Desta maneira, repetindo indefinidamente essas iterações, o Floco de Neve de Koch é definido como sendo a figura que se obteria, caso o processo recursivo das iterações nunca acabasse, conforme descrito na Figura 4.

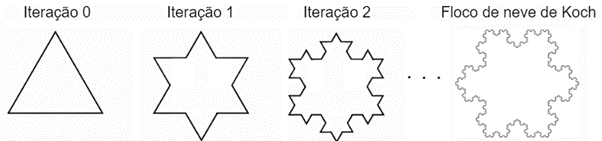
Figura 4 - Processo recursivo de Koch: triângulo equilátero.
Fonte: Autores (2023)

A propriedade matemática em que a mesma forma pode se repetir sucessivamente em escalas cada vez menores é conhecida como autossimilaridade. A partir de agora, quando observar como os galhos das árvores se bifurcam várias vezes, repetindo esse processo de formas sucessivas em escalas cada vez menores, ou na forma como os vasos sanguíneos são distribuídos em nosso corpo, será impossível não pensar em Matemática, não é mesmo?