Olá, caros leitores!

Nesta semana estaremos tirando uma dúvida matemática do nosso leitor Victor Hugo, que gostaria de saber um pouco mais sobre as famosas constantes matemáticas $\pi$ e $e$. Para nos ajudar, contaremos com o professor Marcos do nosso querido IFMG - Bambuí.

Qual a origem das famosas constantes matemáticas $\pi$ e $e$?

Por Marcos Alves de Farias (marcos.farias@ifmg.edu.br)

Num primeiro contato, as constantes matemáticas $\pi$ e $e$ nos são apresentadas no Ensino Básico. Geralmente a primeira que descobrimos é a constante, que é representada pela letra grega $\pi$ (pi), cujo estudo está relacionado, dentre outras coisas, aos cálculos de comprimento e área de circunferências, estudos esses que se iniciam ainda no Ensino Fundamental. Já a constante $e$, conhecida como número de Euler, ou número de Napier, dentre outros nomes, é geralmente abordada no Ensino Médio, quando estudamos os logaritmos e suas propriedades.

Uma característica comum entre as duas constantes, $\pi$ e $e$, é que se tratam de números irracionais, ou seja, numericamente, possuem uma representação decimal infinita e não periódica,

$\pi=3,14159265358979 \cdots$   e   $e=2,71828182845905 \cdots$.

Por não periódica entendemos que na expansão decimal desses números não há um “bloco” numérico que se repete, como acontece com os números racionais, por exemplo,

$\frac{1}{3}=0,33333\cdots$;   $\frac{311}{99}=3,141414\cdots$   e   $\frac{30173}{11100}=2,718288288288\cdots$.

Iniciando pela constante $\pi$, caso fossemos capazes de medir o perímetro, que corresponde ao comprimento, de uma circunferência “qualquer”, tendo essa medida representada pela letra $C$ e o comprimento do seu raio representado pela letra $R$, teríamos que

$\pi=\frac{C}{2R}$.

Isto é, o valor de $\pi$ corresponde exatamente à razão entre o perímetro de uma circunferência e o seu diâmetro.

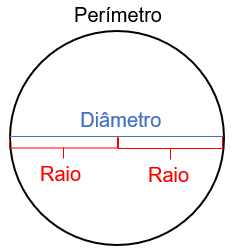
Circunferência com as suas medidas em destaque.
Fonte: Próprio autor.

A notação da constante π remete a primeira letra da palavra grega “περίμετρος”, cujo significado é perímetro, e por sua relação com a circunferência tal constante é também conhecida como constante circular, ou número de Ludolph, em homenagem ao matemático alemão Ludolph Van Ceulen (1540 – 1610), pelos seus estudos com aproximações numéricas para essa constante.

Sendo $\pi$ a constante matemática mais antiga que se tem registro, não é uma tarefa fácil descrever com perfeição suas origens, de certo devem estar relacionadas com cálculos que envolvem medidas circulares. Segundo historiadores matemáticos, por volta de 4.000 a 3.000 a.C. já se tinha ciência sobre a relação de proporcionalidade entre o perímetro de uma circunferência e o seu diâmetro. Os documentos mais antigos que se tem conhecimento sobre os valores de $\pi$ são tábuas mesopotâmicas datadas de 2.000 a.C., que utilizavam como aproximação grosseira $\pi=3$.

Diferente da constante $\pi$, do qual já se tinha conhecimento desde a Antiguidade, a constante $e$ só veio a ser descoberta na Idade Moderna. Ao longo da história há vários contextos independentes que levaram ao surgimento dessa constante, sendo o primeiro deles os logaritmos de Napier.

O escocês John Napier (1550 – 1617) não era um matemático profissional, mas era um estudioso que se interessava por diversos assuntos, dentre eles, alguns ramos da Matemática. Estudando algumas sequências numéricas, estabeleceu os primeiros conceitos sobre logaritmos, numa base em que na época não foi capaz de definir. Hoje se sabe que a base trabalhada por Napier era $\frac{1}{e}$, fato este que tornou a constante $e$ conhecida com número de Napier, ou número de Neper, ou número neperiano.

Estudando problemas matemáticos de ordem financeira, Jacob Bernoulli (1654 – 1705) encontrou uma relação entre a constante $e$ e os conceitos de juros compostos. Observe, que sendo

$M=C(1+i)^t$,

a fórmula que cálcula o valor do montante $M$ ao se investir um capital $C$ por um tempo $t$, a juros compostos com uma taxa de $i$%, se um capital de R$ 1,00 fosse investido num período de 1 ano a uma taxa de 100% ao ano, teríamos como montante ao final da aplicação o valor

$M=1(1+1)^1=2$.

Agora, num problema parecido, se o capital de R$ 1,00 fosse investido num período de 1 ano a uma taxa de 50% por semestre, então

$M=1(1+\frac{1}{2})^2=2,25$.

Caso o capital de R$ 1,00 fosse investido num mesmo período de 1 ano a uma taxa de 25% por trimestre, teríamos que

$M=1(1+\frac{1}{4})^4=2,44140625$.

Prosseguindo com este problema, supondo que o mesmo capital recebesse $n$ capitalizações num período de 1 ano de investimento, obteríamos a seguinte fórmula matemática para o montante

$M=(1+\frac{1}{n})^n$.

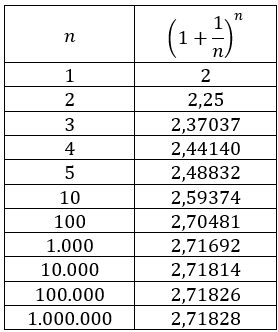
Observe a tabela abaixo, em que consta o valor de $(1+\frac{1}{n})^n$ com cinco casas após a vírgula para diferentes valores de $n$, e perceba que à medida em que se aumentam os valores de $n$, os valores de  $(1+\frac{1}{n})^n$ ficam cada vez mais próximos da constante $e=2,71828182845905 \cdots$. Neste contexto, em notação matemática, surge o conceito de limite, que se escreve por

$\displaystyle\lim_{n\rightarrow +\infty}\left(1+\frac{1}{n}\right)^n=e$,

de maneira que tal limite pode ser usado para definir precisamente quem seria a constante $e$.

Dentre todos os nomes que são atribuídos à constante $e$, certamente, o “número de Euler” é o mais conhecido. Isso se deve a grande fama e importância do matemático suíço Leonhard Euler (1707-1783), que em seus trabalhos com os logaritmos foi o primeiro a utilizar a notação $e$ para essa constante, em alusão possivelmente a palavra exponencial, cuja escrita em latim é exponentialis.

Um fato curioso, segundo consta nos livros sobre histórias da Matemática, é que o uso definitivo da letra grega $\pi$ para a constante circular também se deveu ao Euler, em que apesar de não ter sido o primeiro a utilizar a notação, foi apenas a partir do uso em um de seus trabalhos que a tornou largamente conhecida e utilizada.