Por Marcos Alves de Farias (marcos.farias@ifmg.edu.br)

Como teto de pagamentos de aposentadoria, o Instituto Nacional do Seguro Social (INSS), que é responsável pelo pagamento da aposentadoria de boa parte dos brasileiros, limita atualmente ao valor mensal de R$7.786,02, mas é sabido que boa parte dos nossos aposentados sobrevivem com muito menos.

Uma maneira de garantir a saúde financeira na terceira idade é a criação de uma previdência complementar, que visa a construção de um fundo monetário para a remuneração futura do trabalhador, quando chegar o momento de sua aposentadoria.

Em geral, a criação de uma previdência está relacionada ao seguinte problema: dados um valor mensal, que se deseja receber, e uma taxa de juros de rendimento, quais devem ser os depósitos mensais a serem aplicados, durante o período de trabalho, para que esteja garantida no futuro as retiradas pretendidas?

Esse problema envolve a aplicação dos juros compostos, um conteúdo da Matemática Financeira.

Para melhor exemplificar, primeiro trataremos de um exemplo particular e depois desenvolveremos uma fórmula matemática geral aplicável a qualquer caso que se apresentar.

Problema particular: Um profissional, atualmente com 30 anos, pretende se aposentar aos 65 anos e deseja receber uma complementação de aposentadoria de R$5.000,00 durante 25 anos. Qual deve ser o valor dos depósitos mensais que deverá efetuar para atingir o seu objetivo, considerando que o fundo criado contará com um rendimento de 0,5% ao mês, que historicamente é o que corresponde a caderneta de poupança?

A solução do problema está relacionada a duas perguntas:

1) Qual é a quantia  que, aplicada a taxa de 0,5% ao mês, pode gerar uma retirada de R$5.000,00 durante 300 meses (25 anos)?

2) Qual é o valor mensal  que, aplicado à taxa de 0,5% ao mês, acumulará ao final de 420 meses (35 anos) a tal quantia?

Solução: Para responder as perguntas, começamos lembrando que um capital empregado a juros composto com uma taxa de 0,5% ao mês, valerá, ao final do 1° mês,

Ao final do 2° mês,

e, assim por diante, ao final de $n$ meses,

$$C_n=1,005^n C.$$

Então, num período de 420 meses, o valor fixo dos depósitos mensais acumulará o montante de

e utilizando a fórmula da soma dos termos de uma Progressão Geométrica (PG), obtemos

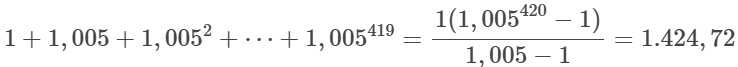
implicando em

$$M=1.424,72C.$$

Por outro lado, este $M$ deve ser o valor que aplicada a taxa de 0,5% ao mês gerará retiradas mensais de R$5.000,00 durante 300 meses (25 anos). Isto é,

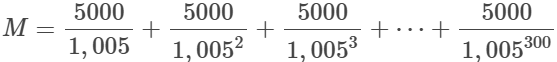
que, mais uma vez pela fórmula da soma de PG,

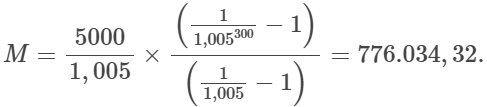
Por fim, equacionando

$$1.424,72C=776.034,32$$

encontramos

$$C=\frac{776.034,32}{1.424,72}=544,70$$

que deve ser os valores mensais depositados.

Problema geral: Para que um profissional tenha uma complementação mensal de aposentadoria no valor de $R$, por um período de $m$ meses, qual deve ser o valor fixo $C$ das contribuições que deverá ser aplicado durante $n$ meses a uma taxa de rendimento de $i$ (por cento) ao mês?

Solução: Seguindo a ideia anterior, o montante acumulado será

Então, utilizando a fórmula da soma de PG, encontramos  

$$M=\frac{C[(1+i)^n-1]}{i}.$$

Por outro lado, este $M$ deve ser o valor que possibilitará as retiradas mensais de $R$ durante $m$ meses. Portanto,

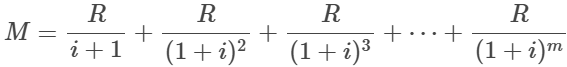
que, pela fórmula da soma de PG,

$$M=\frac{R[(1+i)^m-1]}{i(1+i)^m}.$$

Assim, igualando as duas fórmulas que encontramos para $M$,

$$\frac{C[(1+i)^n-1]}{i}=\frac{R[(1+i)^m-1]}{i(1+i)^m}$$

obtemos

$$C=\frac{R[(1+i)^m-1]}{(1+i)^m[(1+i)^n-1]}.$$

Observe que tomando $R=5000$, $i=0,5\%=0,005$, $m=300$ e $n=420$, solucionaremos o problema particular que apresentamos anteriormente. Isto é,

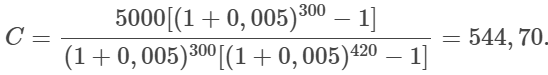
Por fim, informamos ao leitor menos familiarizado com a Matemática Financeira, que pode ter achado confuso alguns dos cálculos apresentados, que a fórmula mais relevante é a que se apresenta ao final para o cálculo do $C$. Perceba que esta é uma fórmula composta de operações aritméticas, tais como soma, subtração, multiplicação, potenciação e divisão, que podem facilmente serem calculadas com o auxíliio de uma calculadora.