Por Marcos Alves de Farias (marcos.farias@ifmg.edu.br)

Frequentemente em Matemática, seja para o cálculo do Mínimo Múltiplo Comum (MMC) ou do Máximo Divisor Comum (MDC), somos obrigados a decompor os números inteiros em produtos de fatores primos. Para isso, uma dificuldade que normalmente surge, quando o número a ser decomposto é grande e não dispomos de calculadora, é se tal número é divisível ou não por determinado número primo. Ciente desta dificuldade, o objetivo deste texto será o de apresentar critérios que implicam em divisibilidade para todos os números primos positivos até 100, que seriam:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.

Um critério de divisibilidade é uma regra, que se satisfeita, implicará em determinado número ser divisível por um outro, sem que para isso precisemos efetuar tal divisão. Para os três primeiros números primos, a divisibilidade pode ser facilmente constatada, uma vez que é sabido que um número é divisível por 2, apenas se ele for par. Quanto ao número 3, é também de conhecimento dos alunos do Ensino Fundamental que um número é divisível por 3 apenas se a soma dos seus algarismos for divisível por 3. Por exemplo, 891 é divisível por 3, pois 8+9+1=18 e 18 é divisível por 3. Já para o número 5, um número é divisível por ele apenas se termina em 0 ou em 5. Deste modo, focaremos em nosso texto na apresentação de critérios de divisibilidade para os primos de 7 a 97.

Para a utilização dos critérios que apresentaremos é importante que antes compreendamos alguns conceitos. Fixado um determinado número inteiro $n$, deixemos definido que a letra $a$ representará o seu algarismo da unidade e a letra $b$ os demais algarismos que o compõe, o que implica escrever $n=ab$.

Exemplos:

a) Se $n=24$, então $a=2$ e $b=4$.  

b) Se $n=192$, então $a=19$ e $b=2$. 

c) Se $n=57940$, então $a=5794$ e $b=0$.

Tabela 1: Critérios de divisibilidade

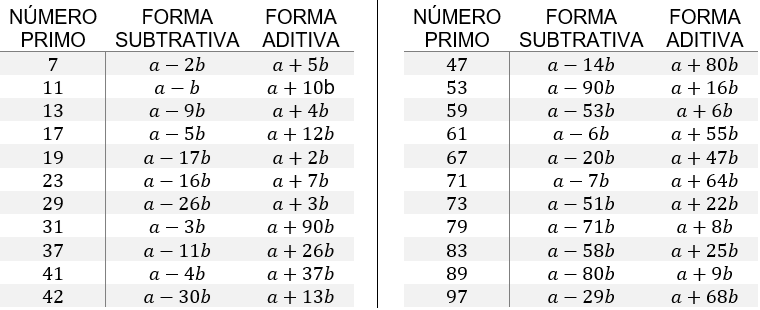
Em síntese, os critérios de divisibilidade consistirão em verificar se um dado número inteiro $n$, que deverá ser lido como $n=ab$, é divisível ou não por um certo número primo. Na Tabela 1 há três colunas a considerar, a primeira diz respeito ao número primo que desejaremos verificar se divide o número $n=ab$. A segunda coluna, chamada de Forma Subtrativa, diz respeito a uma expressão matemática, que envolve a operação de subtração, em que se o resultado gerar um número que é divisível pelo primo, então o número $n$ também será divisível por esse primo. Por fim, a terceira coluna, chamada de Forma Aditiva, funciona de modo análogo a Forma Subtrativa, mas ao invés da subtração, a operação utilizada é a adição.

Observe que para cada número primo, a Tabela 1 propõe 2 formas diferentes de se examinar a divisibilidade, uma por meio da Forma Subtrativa e outra por meio da Forma Aditiva. Daí, caberá ao aluno escolher a forma de sua preferência.

Exemplos:

a) Verifique se o número 91 é divisível por 7.

Forma Subtrativa: se $n=91$, segue que $a=9$ e $b=1$. Então, como $a-2b=9-2\times 1=7$, sendo 7 divisível por 7, conclui-se que 91 é divisível por 7.

Forma aditiva: se $n=91$, segue que e $a=9$ e $b=1$. Então, como $a+5b=9+5\times 1=14$, sendo 14 divisível por 7, conclui-se que 91 é divisível por 7.

Observação: Perceba, no próximo exemplo, que as regras podem ser utilizadas diversas vezes seguidas até que se chegue a um número de fácil verificação.

b) Verifique se o número 3608 é divisível por 11.

Forma Subtrativa: se $n=3608$, segue que $a=360$ e $b=8$. Então, como $a-b=360-8=352$, podemos aplicar o critério de novo para $a=35$ e $b=2$ e obter que $a-b=35-2=33$. Por fim, sendo 33 divisível por 11, conclui-se que 3608 é divisível por 11.

Forma Aditiva: se $n=3608$, segue que $a=360$ e $b=8$. Então, como $a+10b=360+10\times 8=440$, podemos aplicar o critério de novo para $a=44$ e $b=0$ e obter que $a+10b=44+10\times 0=44$. Por fim, sendo 44 divisível por 11, conclui-se que 3608 é divisível por 11.