Por Letícia Alves da Silva; Marcos Alves de Farias (marcos.farias@ifmg.edu.br); Samuel Leandro Fonseca Amaral; Wesley Isidoro de Paula.

Você conhece os conjuntos numéricos? Se conhece, acreditaria se contássemos que o conjunto dos números naturais possui, de certa maneira, a mesma quantidade de números que o conjunto dos inteiros? Neste texto, discutiremos tal fato! Agora, caso não se lembre dos conjuntos numéricos, não haverá problema, pois os apresentaremos também!

É no ensino básico que iniciamos os estudos dos conjuntos numéricos. O conjunto dos números naturais é o primeiro que estudamos, sendo denotado por

$$\mathbb{N}=\left\{0,1,2,3,4,5,6,7,8,9,10,11,\cdots\right\},$$

ele se constitui dos números que utilizamos para contar.

Não é difícil perceber que o conjunto dos números naturais é inapropriado para a realização de subtrações, pois a diferença de dois desses números pode não ser um número natural. Por exemplo, a subtração $2-3$ produz como resultado o número negativo $-1$, que não está em $\mathbb{N}.$

O segundo conjunto que estudamos, o dos números inteiros, denotado por

$$\mathbb{Z}=\left\{\cdots, -3,-2,-1,0,1,2,3,\cdots\right\},$$

corrige a falha que os naturais têm com a subtração, uma vez que os números negativos também estão em $\mathbb{Z}$. Contudo, o conjunto dos inteiros se mostra ineficiente para a realização de divisões, pois, como exemplo, perceba que os números $1$ e $2$, apesar de estarem em $\mathbb{Z}$, o resultado da divisão de $1$ por $2$, que é $0,5$, não está!

O problema de $\mathbb{Z}$ com a divisão é corrigido pelo conjunto dos números racionais, que é representado por

$$\mathbb{Q}=\left\{\frac{a}{b}\mid a,b\in\mathbb{Z}, \textrm{ com }b\neq 0\right\}.$$

Este é o conjunto dos números que podem ser escritos na forma de uma fração de inteiros, como por exemplo, 

$0=\frac{0}{1}$;  $2=\frac{2}{1}$;  $0,5=\frac{1}{2}$; $0,333 \ldots =\frac{1}{3}$;  $-1,41666 \ldots =\frac{-17}{12}$.

Os números que possuem uma representação decimal infinita e não periódica, como o número $\pi=3,141592 \ldots$, por exemplo, não podem ser escritos na forma de fração de inteiros e, portanto, não são racionais. Tais números são chamados de irracionais e o seu conjunto é denotado por $\mathbb{I}$.

Por fim, englobando todos os conjuntos citados, temos o conjunto dos números reais, que é representado por $\mathbb{R}$.

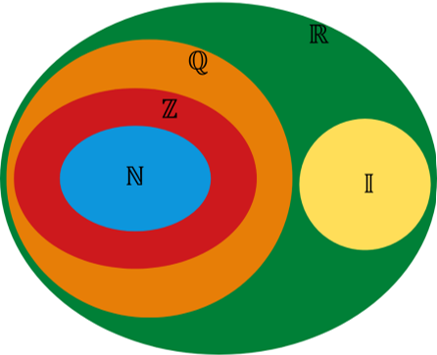
Figura 1 - Diagrama de inclusões dos conjuntos numéricos.
Fonte: Autores (2022).

De modo geral, um conjunto pode ser finito ou infinito. Se um conjunto é finito, a sua cardinalidade é definida como o seu número de elementos. Por exemplo, para o conjunto $A=\left\{-2,0,3,7,11\right\}$, a sua cardinalidade é 5. Para um conjunto que é infinito, como os conjuntos numéricos $\mathbb{N}$, $\mathbb{Z}$ ,$\mathbb{Q}$, $\mathbb{I}$  e $\mathbb{R}$, o conceito de cardinalidade também pode ser definido.

Quando dois conjuntos $A$ e $B$ possuem uma relação, em que cada elemento $x$ de $A$ se corresponde com um único elemento $y$ de $B$, e vice-versa, chamamos essa relação de correspondência biunívoca. Por exemplo, se $A=\left\{1,2,3,4,5\right\}$ e $B=\left\{a,b,c,d,e\right\}$, então a relação de $A$ para $B$, apresentada como

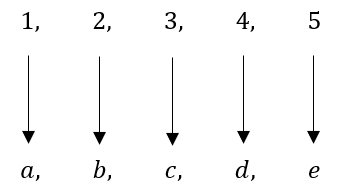
que corresponde a função $f:A\rightarrow B$, definida por

$f(1)=a$,  $f(2)=b$,  $f(3)=c$,  $f(4)=d$,  $f(5)=e$,

representa uma correspondência biunívoca, que pode também ser chamada de bijeção.

Para dois conjuntos finitos, se eles estão em correspondência biunívoca, então certamente possuem o mesmo número de elementos, isto é, a mesma cardinalidade.

Também é possível estabelecer relações biunívocas entre conjuntos infinitos e, naturalmente, a cardinalidade neste contexto é definida de modo que conjuntos com este tipo de correspondência tenham a mesma cardinalidade.

Curiosamente, embora os números negativos não estejam em $\mathbb{N}$, os conjuntos $\mathbb{N}$ e $\mathbb{Z}$ possuem a mesma cardinalidade e a função $f:\mathbb{N}\rightarrow \mathbb{Z}$, dada por

que associa os números pares de $\mathbb{N}$ aos não negativos de $\mathbb{Z}$ e os ímpares de $\mathbb{N}$ aos negativos de $\mathbb{Z}$, conforme apresentado no diagrama a seguir, mostra que os conjuntos $\mathbb{N}$ e $\mathbb{Z}$ possuem a mesma cardinalidade, ou seja, que de certa maneira, possuem a mesma quantidade de elementos. 

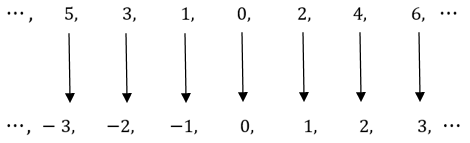
Quando existe uma bijeção entre $\mathbb{N}$ e um outro conjunto $A$, é dito que $A$ é enumerável. Logo, deve-se concluir que $\mathbb{Z}$ é enumerável. Com um argumento mais sofisticado, pode-se verificar que $\mathbb{Q}$ é enumerável também. Já o conjunto $\mathbb{R}$ dos números reais não é enumerável, possuindo assim uma cardinalidade diferente de $\mathbb{N}$, $\mathbb{Z}$ e $\mathbb{Q}$, o que mostra, portanto, que existem diferentes tipos de infinito, mas deixaremos essa discussão para um próximo “Você sabia?”.