Por Letícia Alves da Silva (leticia.alves@ifmg.edu.br) e Fábio Pires Mourão (fabio.mourao@ifmg.edu.br)

Reza a lenda que uma princesa, diante do desafio de obter a maior área de terra com o couro de um boi, inteligentemente, fez uma corda com o material e mediu um semicírculo próximo à margem de um rio. Você faria o mesmo?

Já nos primeiros anos escolares, aprendemos a calcular as medidas de área (A) e do perímetro (P) de algumas figuras planas, como por exemplo de um retângulo:

Figura 1: A figura ilustra um retângulo de dimensões b e h, com medida de área A = b x h e de perímetro P = 2b + 2h.

Suponha então que pretendamos construir um canteiro retangular, dispondo de uma corda (que definirá o contorno do canteiro), com medida de comprimento P = 8m. Vejamos algumas opções:

Figura 2: A figura ilustra retângulos de dimensões (em metros)  2 x 2, 3 x 1, 2,5 x 1,5, com suas respectivas medidas de área.

Embora estes retângulos satisfaçam P = 8m, eles possuem medidas de área distintas. Dentre estas três opções, a que possui maior medida de área é o retângulo cujas dimensões são b = h = 2m, ou seja, o quadrado cujo lado mede 2m.

Podemos encontrar outro retângulo, com P = 8m, mas com medida de área superior a 4m²? Será a medida de área máxima 4m²?

Este é um problema de otimização, onde desejamos maximizar uma função (que fornece a medida de área do retângulo), com uma restrição (o perímetro deve medir 8m). Ademais, os valores de b e h devem ser maiores que 0 (e, consequentemente, menores que 4), pois serão as dimensões de um retângulo. Matematicamente, escrevemos:

Maximizar A = b x h.

Sujeito a P = 2b + 2h = 8,

b, h > 0.

Observe que, se 2b + 2h = 8, então b + h = 4 e h = 4 – b. Logo, podemos reescrever a função como A = b x h = b x (4 – b) = -b² + 4b, passando assim a enxergar A como a função do segundo grau A(b) = - b² + 4b, cujo gráfico é a parábola:

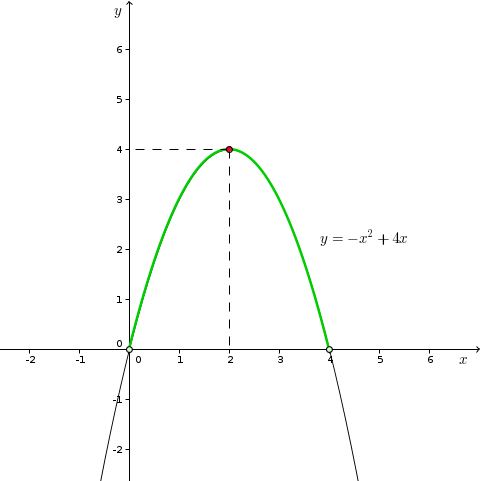
Figura 3: A figura destaca o gráfico da função quadrática y = - x² + 4x, no intervalo aberto de 0 a 4.

Aqui, $x$ representa o comprimento da base b (em metros) e $y$ representa a área (em metros quadrados) do retângulo de base b e altura 4-b.

Em $x$ = b = 2, temos o valor máximo para $y$ = A($x$), que é $y$ = 4. Portanto, a área do canteiro retangular com medida do perímetro P = 8m será máxima quando a medida da base for b = 2m (e consequentemente, h = 2m).

Imagine agora que possamos construir o canteiro no formato de outra figura plana, mas mantendo-se P = 8m.

O perímetro de um círculo de raio r mede P = 2πr. Assim, para que tenhamos P = 8m, o raio do círculo deverá ser tal que 2πr = 8m, donde r = 4/π m. Considerando o valor de π aproximadamente 3,14, a medida de área do canteiro circular será de aproximadamente A = πr² $\approx$ 5,095 m².

Logo, dentre todos os retângulos e o círculo, cujos perímetros medem 8m, o círculo possui maior medida de área. Não satisfeitos, podemos ainda nos perguntar se existe alguma outra região plana, limitada por uma curva fechada de 8m, mas que tenha uma medida de área superior a do círculo.

A resposta é não, pois pela afamada Desigualdade Isoperimétrica: para o comprimento P de uma curva fechada e a área A da região plana que ela envolve, temos que:

$$4\pi A\leq P^2,$$

valendo a igualdade se e só se a curva é uma circunferência.

Isso significa que A ≤ P² /(4π), e quando P=8m, obtemos:

$$A\leq \frac{64}{4\pi} m^2\approx 5,095 m^2.$$

Vale destacar que a desigualdade isoperimétrica possui muitas aplicações na Matemática e em outras áreas. Esta é a sua versão no plano, mas ela pode ser enunciada de forma mais geral, no espaço n-dimensional.

E quanto à princesa? Podemos utilizar a desigualdade isoperimétrica para concluir que ela tomou a melhor decisão. Pense nisso!