Por Letícia Alves da Silva (leticia.alves@ifmg.edu.br); Marcos Alves de Farias; Samuel Leandro Fonseca Amaral; Wesley Isidoro de Paula.

Existem afirmações que, embora pareçam triviais, nos levam a conclusões bastante interessantes. Neste texto, discorreremos sobre uma delas.

Comecemos com algumas perguntas. Qual é a letra inicial do seu nome? Na sua sala de aula há (ou havia - caso já tenha se formado) alguém cujo nome também comece com a letra inicial do seu nome? Ou ainda: Existem pelo menos duas pessoas cujos nomes comecem com a mesma letra?

Se em sua sala de aula há mais de 26 alunos, a resposta para a última pergunta certamente foi “sim”. Como podemos saber disso? A resposta é dada pelo Princípio da Casa dos Pombos, também conhecido como Princípio das Gavetas de Dirichlet.

Este princípio afirma que “se n+1 pombos devem ser postos em n casas, então pelo menos uma casa irá conter mais de um pombo”.

Note que, ao pensarmos nas 26 letras do alfabeto como n = 26 casas, havendo 27 ou mais alunos e, portanto, 27 ou mais nomes, haverá pelo menos uma letra que será a inicial de mais de um nome.

Este princípio, embora de enunciado simples, pode ser utilizado para resolver muitos problemas. Vejamos outro exemplo:

Qual a quantidade mínima de pessoas necessária em um grupo para que, com certeza, existam pelo menos duas pessoas que façam aniversário no mesmo mês?

A resposta é 13 pessoas. De fato, ao pensarmos nos 12 meses como 12 casas e nas pessoas como os pombos que precisam ser alocados nas casas (de acordo com o mês em que fazem aniversário), segue pelo Princípio da Casa dos Pombos, que haverá ao menos um mês com duas pessoas celebrando o aniversário no mesmo mês.

Este princípio também pode ser utilizado para resolver problemas essencialmente matemáticos como, por exemplo, para provar que:

Considerando um quadrado cujo lado mede 2 u.c. (unidades de comprimento), dados 5 pontos quaisquer sobre a superfície deste quadrado, certamente existirá dois destes pontos que estarão a uma distância de no máximo raiz quadrada de 2.

De fato, podemos dividir o quadrado original em quatro quadrados cujos lados medem 1 u.c., conforme é mostrado na Figura 1 abaixo.

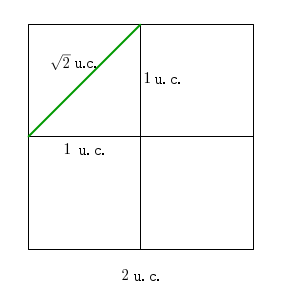
Figura 1: Representação geométrica do problema.
Fonte: Próprios autores.

Pensando agora nos quatro quadrados como quatro casas e nos 5 pontos na superfície do quadrado original como pombos postos nas quatro casas, pelo Princípio da Casa dos Pombos, haverá ao menos um quadrado cujo lado mede 1 u.c. em que existirá dois pontos. Mas a distância máxima entre dois pontos sobre a superfície deste quadrado é dada pela medida de comprimento da diagonal, que é $d=\sqrt{1^2+1^2}$ $=\sqrt{2}$ u.c.

Portanto, este princípio pode ser aplicado em várias situações que envolvem raciocínio lógico-matemático. Pense em outros problemas que possam ser resolvidos através deste princípio e proponha divertidos desafios aos seus amigos!